Chemical Engineering Mock Interview 2

Mock interview questions covering dimensional analysis, mathematical functions, and biotechnology applications

7 questions • Estimated time: 45-60 minutes

How to Use This Mock

Read each question carefully
Attempt your own answer first — spend at least 5 minutes thinking
Only reveal the model answer after you've tried
Compare your reasoning to the model answer

Dimensional Analysis, Fluid Mechanics

Some physical phenomena are extremely challenging to model, but we can get a long way using dimensional analysis. This is the idea that if an equation exists it must also exist in a dimensionless form. This can dramatically reduce the number of variables that need to be considered.

Spherical pharmaceutical pellets discharge from a circular orifice of diameter $D$ at the base of a cylindrical bunker. A steady gauge pressure $P$ is applied by air at the top of the bunker, resulting in a mass flowrate $W$ of pellets.

The flowrate depends on: bulk density of pellets $\rho$ , pellet diameter $d$ , orifice diameter $D$ , applied pressure $P$ , and gravitational acceleration $g$ .

Part (a): First, let's identify what dimensions each of these quantities has. Can you write down the dimensions of $W$ , $\rho$ , $d$ , $D$ , $P$ , and $g$ ?

Model Answer

Mass flowrate $W$ has dimensions of mass per time, so $[W] = M T^{-1}$ . Density is $[\rho] = M L^{-3}$ . Both diameters are lengths: $[d] = [D] = L$ . Pressure is force per area, so $[P] = M L^{-1} T^{-2}$ . Gravity is $[g] = L T^{-2}$ .

Key Concepts:

Dimensional analysisPhysical dimensions

Dimensional Analysis, Fluid Mechanics

Part (b): We have 6 variables and 3 dimensions, so we expect $6 - 3 = 3$ dimensionless groups. There are lots of ways you can do this, but today let's look for three groups based on $d$ , $P$ and $W$ . How would you construct these?

Model Answer

Initial hypothesis:

We could combine variables to cancel out dimensions?

$\Pi_1 = \frac{d}{D},$

$\Pi_2 = \frac{P}{\rho g D},$

$\Pi_3 = \frac{W}{\rho \sqrt{g} D^{5/2}}.$

Possible Approach:

\frac{[W]}{[\rho]^{a}[g]^{b}[D]^{c}} = 1,

M T^{-1} = (M L^{-3})^{a} (L T^{-2})^{b} (L)^{c},

M: 1 = a + b,\quad T: -1 = -2b, \quad L:0 = -3a + c

so $a=1$ , $b=1/2$ , $c = 5/2$

Key Concepts:

Dimensionless groupsDimensional cancellation

Dimensional Analysis, Fluid Mechanics

Part (d): Now express your result as a relationship for $W$ in terms of the other variables and an unknown function.

Model Answer

Initial hypothesis:

The dimensionless groups must be related somehow?

Interviewer Nudge:

Yes. Dimensional analysis tells us that $\Pi_3$ must be some function of $\Pi_1$ and $\Pi_2$ . Write this out.

Final answer:

\frac{W}{\rho \sqrt{g} D^{5/2}} = f\left(\frac{P}{\rho g D}, \frac{d}{D}\right)

where

f

is an unknown function. Rearranging:

W = \rho \sqrt{g} D^{5/2} f\left(\frac{P}{\rho g D}, \frac{d}{D}\right).

Interviewer conclusion:

Perfect. Notice how dimensional analysis reduced our problem from 6 variables to just 2 dimensionless parameters. The exact form of $f$ would need to be determined experimentally or from detailed modeling.

Key Concepts:

Functional relationshipsDimensional reduction

Mathematical Analysis

Sketch the function $y = e^x \sin(\pi x)$ .

Model Answer

This is one of those questions you just need to know. The exponential part is called an envelope and this stretches the amplitude of $y=sin(\pi x)$ to touch the functions $y_e = e^x$ and $y_e = -e^x$ . All of the turning points and zero crossings are unchanged in $x$ .

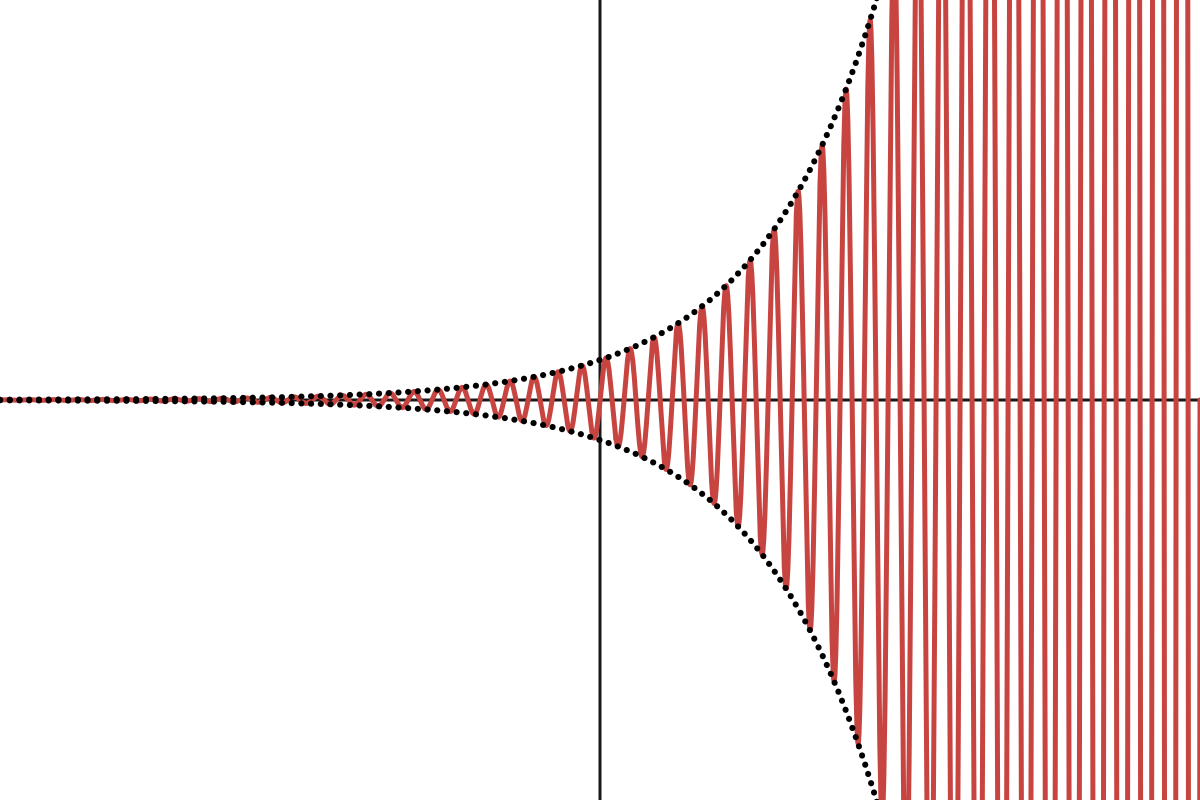
Click to enlarge

Key Concepts:

Exponential growthTrigonometric functionsProduct of functionsEnvelope functions

Biotechnology, Global Challenges

One proposal for addressing climate change is to use algae to capture CO₂ from the atmosphere through photosynthesis.

Part (a): What raw materials would the algae need to grow and capture carbon?

Model Answer

Initial hypothesis:

They'd need CO₂ from the air and sunlight for photosynthesis.

Interviewer Nudge:

Yes, those are key. What else? Think about what plants need to grow.

Refined response:

They'd also need water, and nutrients like nitrogen and phosphorus—similar to fertilizers used in agriculture.

Interviewer follow-up:

Exactly. So we'd need: CO₂, sunlight, water, nitrogen, and phosphorus. Keep these in mind for the next parts.

Key Concepts:

Photosynthesis requirementsNutrient requirementsRaw materials

Biotechnology, Global Challenges

Part (b): Could this algae-based approach be scaled up to make a meaningful impact on atmospheric CO₂? What practical challenges might arise?

Model Answer

Initial hypothesis:

If algae grow quickly, maybe we could just grow lots of them in ponds?

Interviewer Nudge:

Let's think about scale. Global CO₂ emissions are about 40 billion tonnes per year. Even if algae are efficient, what resource might become limiting?

Refined response:

We'd need enormous amounts of water and land. And the nutrients—especially phosphorus—would be a problem. Phosphorus is mined and it's a finite resource. At global scale, we might run out.

Interviewer follow-up:

Good thinking. Also consider: atmospheric CO₂ concentration is about 420 ppm—quite dilute. What does this mean for efficiency?

Final thoughts:

The algae would need to extract CO₂ from very dilute air, which is slow. Maybe it's better to capture CO₂ from concentrated sources like power plant exhaust instead of directly from the atmosphere.

Key Concepts:

Scaling challengesResource limitationsCO₂ concentration effects

Biotechnology, Global Challenges

Part (c): What could go wrong ecologically? And how might you make this economically viable rather than just an expensive carbon removal technology?

Model Answer

Initial hypothesis:

Maybe the algae could escape and cause problems in rivers or oceans?

Interviewer Nudge:

Yes, good point. What specific problems might they cause? Think about ecosystems.

Refined response:

If genetically modified algae escape into natural waters, they might outcompete native species and disrupt the food chain. We'd probably need closed systems—like bioreactors—to contain them, but that's more expensive.

Interviewer follow-up:

Exactly. Now, the algae biomass itself—once you've grown it, what could you do with it to generate revenue?

Final thoughts:

The algae could be processed into useful products: biofuels for energy, animal feed for livestock, or even specialty chemicals. If we can sell these co-products, it helps offset the cost. We might also get carbon credits. But we'd need to check that the energy used for harvesting and processing doesn't exceed the value created.

Key Concepts:

Ecological risksContainment strategiesEconomic viabilityCo-product value

← Back to Chemical Engineering