Chemical Engineering Mock Interview

Mock interview questions covering fluid statics, mathematical analysis, and engineering estimation

6 questions • Estimated time: 45-60 minutes

How to Use This Mock

Read each question carefully
Attempt your own answer first — spend at least 5 minutes thinking
Only reveal the model answer after you've tried
Compare your reasoning to the model answer

Fluid Statics, Thermodynamics

Let's think about how air pressure changes as we go higher in the atmosphere. We know that in any fluid at rest under gravity, the pressure gradient is given by:

\frac{\text{d}P}{\text{d}z} = -\rho g,

where

P

is the pressure,

z

is the height above the ground,

\rho

is the density, and

g

is the gravitational acceleration

Part (a): Assuming that the atmosphere has a constant temperature, $T_0$ , how do you expect $P$ to vary with $z$ ?

Model Answer

Initial hypothesis:

I think we just need to integrate that equation?

Interviewer Nudge:

That's the right instinct, how can we handle the fact that $\rho$ can vary with height?

Refined response:

Oh, I see! Since air is a gas, we could use the ideal gas law:

P = \frac{\rho RT}{M},

where

M

is the molar mass. So,

\rho = \frac{PM}{RT_0}.

Substituting this in:

\frac{\text{d}P}{\text{d}z} = \frac{-PMg}{RT_0}.

This separates:

\frac{\text{d}P}{P} = -\frac{Mg}{RT_0} \text{d}z.

So in the end I get:

P(z) = P_0 \exp \left(-\frac{Mgz}{RT_0}\right),

where

P_0

is the pressure at ground level.

Key Concepts:

Hydrostatic pressure balanceIdeal gas lawExponential atmosphere

Fluid Statics, Thermodynamics

Part (b): Your expression for $P(z)$ introduces a characteristic vertical lengthscale. What does this tell you about why we don't notice pressure changes when standing up?

Model Answer

Initial hypothesis:

Is it just... $RT_0/Mg$ ?

Interviewer Nudge:

Yes, exactly. This is called the scale height. Now let's get physical intuition: what does this length represent, and can you estimate its value?

Refined response:

Let me see... $M \approx 0.029$ kg/mol, $R = 8.314$ J/(mol·K), $T_0 = 300$ K, $g = 10$ m/s². So

H \approx \frac{10 \times 300}{0.03 \times 10} = 10,000\text{m}

, *Note: make your life easy with approximations if you don't have a calculator

Interviewer follow-up:

Excellent calculation. So the pressure changes by a factor of about $1/e \approx 0.36$ for every 10 km you go up.

Final answer:

So if you stand up, you only move about a meter, that's 1/10,000 of the characteristic lengthscale. That's why we don't feel lightheaded or notice any difference when standing up from pressure changes alone.

Key Concepts:

Characteristic lengthscalesOrder of magnitude estimationPhysical intuition

Fluid Statics, Thermodynamics

Part (c): The assumption of constant temperature is quite poor. In reality, temperature typically decreases with height. Suppose instead:

T(z) = T_0(1 - \alpha z)

where $\alpha > 0$ . How does this modify the relationship between density and pressure?

Model Answer

Initial hypothesis:

We'd just... substitute this temperature into the ideal gas law?

Interviewer Nudge:

Yes, good start. Walk me through it.

Refined response:

From before, $\rho = PM/(RT)$ . But now $T = T_0(1 - \alpha z)$ , so

\rho = \frac{PM}{RT_0(1 - \alpha z)}

and

\frac{\text{d}P}{\text{d}z} = \frac{-PMg}{RT_0(1 - \alpha z)}.

Separating:

\frac{\text{d}P}{P} = \frac{Mg}{\alpha RT_0} \left(\frac{-\alpha}{1 - \alpha z}\right) \text{d}z.

\ln \left(\frac{P}{P_0}\right) = \frac{Mg}{\alpha RT_0} \ln \left(1-\alpha z\right)

which gives us:

P(z) = P_0(1 - \alpha z)^{Mg/RT_0\alpha}.

Key Concepts:

Variable temperature atmosphereSeparable differential equationsIntegration with substitution

Fluid Statics, Thermodynamics

Part (d): Can you show that letting $\alpha \rightarrow 0$ recovers your earlier result?

Model Answer

One definition of the exponential is

e^x = \lim_{n\to\infty} (1 + x/n)^n

and I can rewrite my expression as:

(1 - \alpha z)^{Mg/RT_0\alpha} = \left[(1 - \alpha z)^{1/\alpha}\right]^{Mg/RT_0}.

Letting $1/\alpha = n$ , $n\rightarrow \infty$ as $\alpha \to 0$ so

\lim_{\alpha\to 0} (1 - \alpha z)^{1/\alpha} = \lim_{n\to\infty} (1 - z/n)^n = e^{-z}.

\lim_{\alpha \to 0}\left[(1 - \alpha z)^{Mg/RT_0\alpha}\right] = \left[e^{-z}\right]^{Mg/RT_0} = \exp \left(-\frac{Mgz}{RT_0}\right)

and the whole expression becomes

P(z) = P_0 \exp \left(-\frac{Mgz}{RT_0}\right),

which is exactly our isothermal result!

Interviewer conclusion:

Perfect. And why is this kind of limiting check so valuable in physics and engineering?

Student reflection:

It shows our more complex model correctly simplifies to the simpler case we already understood, which gives us confidence we haven't made errors.

Key Concepts:

Limiting behaviorExponential limit definitionModel validation

Mathematical Analysis

Sketch the function:

y = \frac{1}{x} + x^2

Model Answer

Okay, so I can see this graph is going to have two types of limiting behaviour: close to the origin it will look like $y = 1/x$ and far away it will look like $y = x^2$ , so let me just sketch those curves (dotted lines).

Next I'll have a look for solutions to $y=0$ and I can see that there will only be one at $x=-1$

In terms of turning points, I can differentiate it and set that equal to zero

\frac{\text{d}y}{\text{d}x} = -\frac{1}{x^2} + 2x = 0,

so,

x = \frac{1}{2}^{\frac{1}{3}}

Putting those together I can join the dots to make my sketch

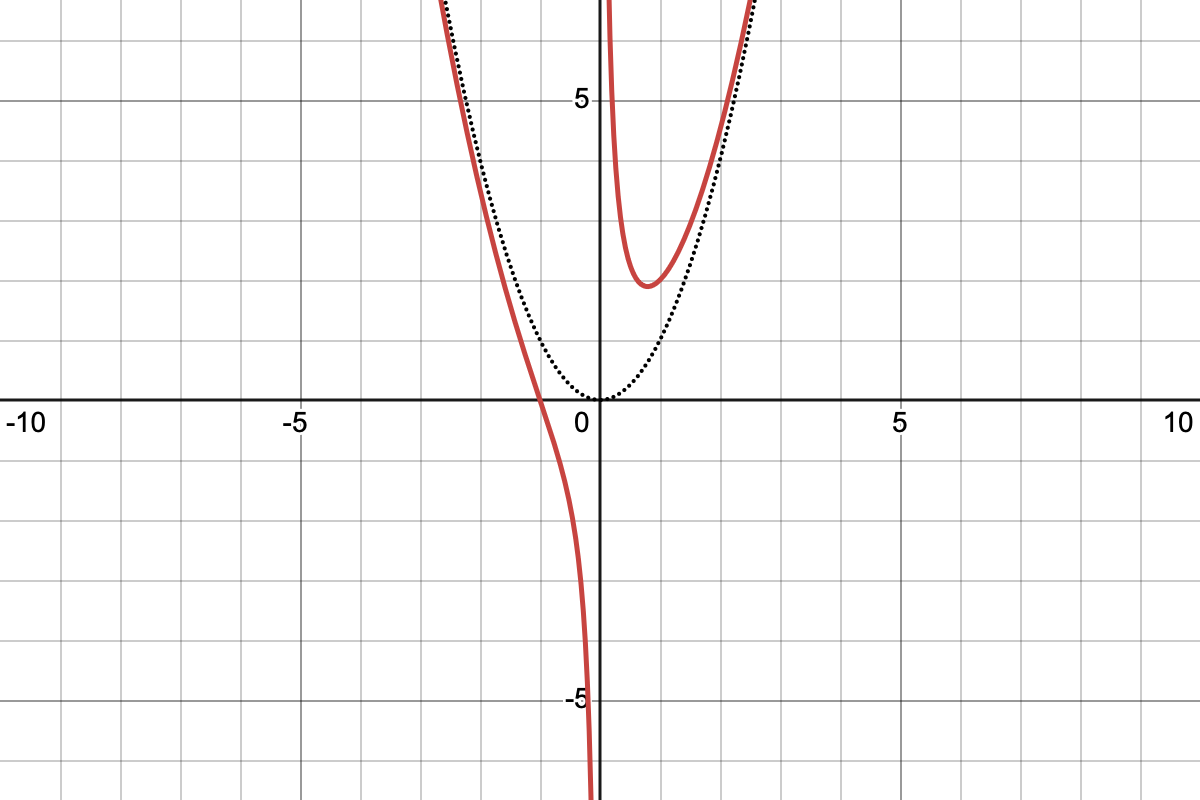
Click to enlarge

Key Concepts:

Asymptotic analysisCritical pointsSecond derivative testFunction behavior

Engineering Estimation, Heat Transfer

A chemical plant has a reactor releasing 100 MW of heat continuously. We need to remove this heat using cooling water. Estimate how much water flow we'd need.

Model Answer

Initial hypothesis:

Maybe thousands of liters per second?

Interviewer Nudge:

Let's work systematically. What equation relates heat transfer rate, mass flow rate, and temperature change?

Refined response:

$\dot{Q} = \dot{m} c \Delta T,$ where $\dot{Q}$ is heat rate, $\dot{m}$ is mass flow, $c$ is specific heat capacity, and $\Delta T$ is temperature rise.

Interviewer follow-up:

Good. Now estimate: what's the specific heat capacity of water, and what's a reasonable $\Delta T$ for industrial cooling?

Student responds:

$c \approx 4,200$ J/(kg·K). For $\Delta T$ , maybe 10°C to avoid scaling and approaching boiling.

Calculation:

So: $\dot{m} = \frac{\dot{Q}}{c \Delta T} = \frac{100 \times 10^6}{4,200 \times 10} = 2,380 \text{ kg/s}.$ Converting to volumetric flow: $\dot{V} = \frac{2,380}{1,000} = 2.38 \text{ m}^3/\text{s} = 2,380 \text{ L/s}.$

Sanity check:

This is equivalent to about 14,000 garden hoses—huge, but reasonable for a 100 MW industrial plant with cooling towers or river access.

Key Concepts:

Energy balanceHeat capacityOrder of magnitude estimationEngineering judgment

← Back to Chemical Engineering